What if your lowest standard is still far from the origin?
You can search the forum for lots of arguments on this. I would encourage you to do that. There's a search box at the top of the page.
For me, the LOQ is the point where you are still sure that you're measuring what you think you're measuring, reliably. I've seen rules of thumb on this where people say "it's a real and reliably measurable signal if it's 10X the noise". I've had instances in my own hands where the S/N ratio was less than 10 and I could reliably measure the signal for the analyte it 10 times in row. In those cases, the mass spec. said it was the target molecule and I could reliably measure it so I had no problems sending out a number on it.
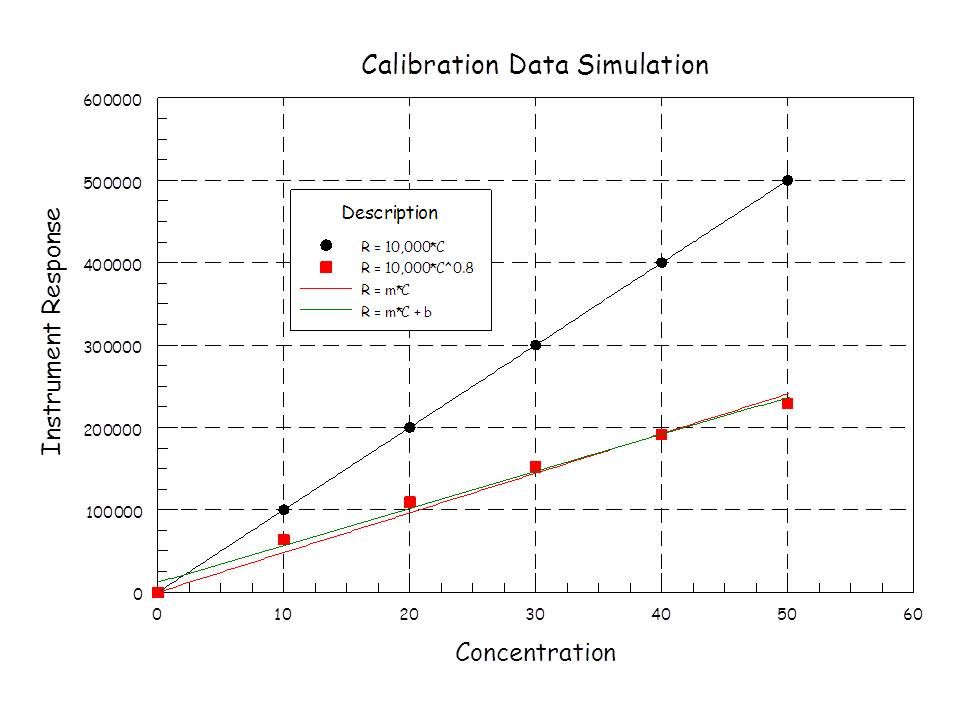
As for that intercept business. In chromatography, at zero concentration, you should have a response that is indistinguishable from the noise of your baseline. If you're really concerned about the low end of the calibrated range, you should be sure to include standards that are way down there. I would include my LOQ standard in the set if I was that concerned. Extrapolating to zero from standards that are far from the origin is not good practice. Including these low-concentration standards will help to guide your intercept toward zero. Mostly, far from the origin, the intercept tells you more about curvature in your calibration data than it does anything else. Ever get a negative intercept? How does that make any physical sense? Generally, it doesn't. Calibration data that is slightly concave upward will give you a negative intercept. If the data is concave downward, you'll get a positive intercept. The y-intercept is actually dictated by the average concentration and average response in your calibration set. That is a point that's relatively far from zero concentration. It doesn't make sense to me to use it. It makes more sense to try to figure out why your calibration data is nonlinear and is giving you a substantial intercept at all.
Here's an example of what I'm talking about. I added a little nonlinearity (5%) to data that should be a perfect straight line, no intercept. Slopes are close to 1 and the correlation coefficients are quite good. Note the sign on the intercepts:

I mostly work at the low-concentration end of my calibrated range. I use the method of standard addition a lot for calibration because my preferred sampling technique is SPME and it's quite matrix dependent. So, LOD and LOQ for me are all about S/N and what's the risk in me reporting something that's not accurate.